Le repère orthonormé 3D : Guide complet pour les étudiants en mathématiques
Introduction
Le repère orthonormé est un outil fondamental en mathématiques, notamment en géométrie et en algèbre linéaire. Il permet de représenter des points, des vecteurs et des plans dans l’espace à trois dimensions. Ce guide complet fournira aux étudiants en mathématiques une compréhension approfondie du repère orthonormé 3D, de sa construction à ses applications.
Construction du repère orthonormé
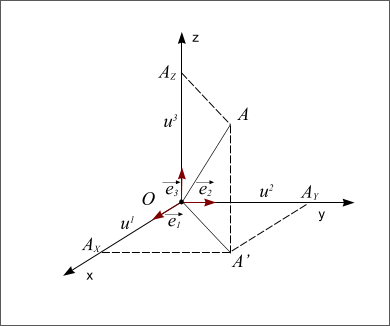
Un repère orthonormé 3D est défini par trois vecteurs unitaires orthogonaux :
- i : vecteur unitaire dans la direction de l’axe des x
- j : vecteur unitaire dans la direction de l’axe des y
- k : vecteur unitaire dans la direction de l’axe des z
Ces vecteurs sont orthogonaux, c’est-à-dire qu’ils forment des angles droits entre eux. Ils sont également unitaires, c’est-à-dire qu’ils ont une longueur de 1.
Coordonnées cartésiennes
Les coordonnées cartésiennes d’un point P dans l’espace 3D sont données par le triplet (x, y, z), où x, y et z sont les distances algébriques de P aux plans yz, xz et xy, respectivement.
Vecteurs
Un vecteur dans l’espace 3D peut être représenté par une combinaison linéaire des vecteurs unitaires i, j et k :
v = xi + yj + zkoù x, y et z sont les composantes du vecteur v.
Applications
Le repère orthonormé 3D a de nombreuses applications en mathématiques, notamment :
- Géométrie analytique : représentation de points, de lignes et de plans dans l’espace
- Algèbre linéaire : résolution de systèmes d’équations linéaires, calcul de déterminants
- Calcul vectoriel : calcul de gradients, de divergences et de rotations
- Physique : représentation des forces, des vitesses et des accélérations
Diagramme
Le diagramme suivant illustre un repère orthonormé 3D :
| Vecteur | Direction |
|---|---|
| i | Axe des x |
| j | Axe des y |
| k | Axe des z |
Conclusion
Le repère orthonormé 3D est un outil puissant qui permet aux étudiants en mathématiques de représenter et de manipuler des objets géométriques et des vecteurs dans l’espace à trois dimensions. Ce guide complet a fourni une compréhension approfondie de la construction, des coordonnées et des applications du repère orthonormé, permettant aux étudiants de maîtriser ce concept fondamental.
Enregistrer un commentaire for "Repère Orthonormé 3D : Guide Pour Les Étudiants En Mathématiques"