Figures Géométriques en 3D : Apprenez à Les Créer et Les Comprendre

Introduction
Les figures géométriques en 3D, aussi appelées solides géométriques, sont des objets mathématiques qui existent dans l’espace tridimensionnel. Elles sont omniprésentes dans notre monde, de la forme d’un cube à celle d’une sphère. Comprendre les figures géométriques en 3D est essentiel dans de nombreux domaines, tels que l’architecture, l’ingénierie, la physique et même l’art.
Cet article vous guidera à travers le monde fascinant des figures géométriques en 3D, vous aidant à les comprendre, à les créer et à les utiliser dans diverses applications.
Définitions Fondamentales
Avant de plonger dans le monde des figures géométriques en 3D, il est important de définir certains termes clés :
- Point: Un point est une position dans l’espace. Il n’a ni dimension ni taille.
- Ligne: Une ligne est une suite infinie de points qui s’étendent dans une seule direction. Elle n’a qu’une dimension : la longueur.
- Plan: Un plan est une surface bidimensionnelle infinie. Il possède deux dimensions : la longueur et la largeur.
- Solide: Un solide est un objet tridimensionnel qui possède trois dimensions : la longueur, la largeur et la hauteur.
Les Différents Types de Figures Géométriques en 3D
Les figures géométriques en 3D peuvent être classées en plusieurs catégories, chacune ayant ses propres propriétés et caractéristiques :
1. Les Polyèdres
Les polyèdres sont des solides dont les faces sont des polygones. Ils sont caractérisés par leurs arêtes, qui sont les segments de droite reliant les sommets, et leurs faces, qui sont les polygones qui forment la surface du solide.

- Prismes: Les prismes sont des polyèdres formés par deux polygones identiques et parallèles, appelés bases, et par des parallélogrammes qui les relient.
- Exemple: Cube, parallélépipède rectangle, prisme triangulaire.
- Pyramides: Les pyramides sont des polyèdres formés par une base polygonale et des triangles qui se rejoignent en un point appelé sommet.
- Exemple: Pyramide carrée, pyramide triangulaire.
- Autres Polyèdres:
- Tétraèdre: Un tétraèdre est un polyèdre à quatre faces triangulaires.
- Octaèdre: Un octaèdre est un polyèdre à huit faces triangulaires.
- Dodécaèdre: Un dodécaèdre est un polyèdre à douze faces pentagonales.
- Icosaèdre: Un icosaèdre est un polyèdre à vingt faces triangulaires.
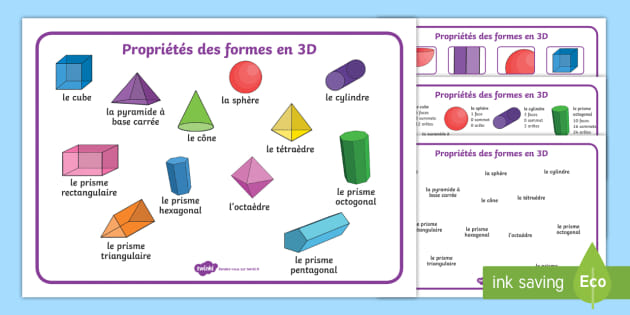
2. Les Corps Ronds
Les corps ronds sont des solides qui ne sont pas formés uniquement de surfaces planes. Ils sont définis par des courbes et des surfaces courbes.
- Sphère: Une sphère est un solide tridimensionnel dont tous les points sont à une distance égale d’un point central appelé centre.
- Cylindre: Un cylindre est un solide formé par deux cercles identiques et parallèles, appelés bases, et par une surface courbe qui les relie.
- Cône: Un cône est un solide formé par un cercle appelé base et par une surface courbe qui se termine en un point appelé sommet.
- Tore: Un tore est un solide en forme de donut, obtenu en faisant tourner un cercle autour d’un axe qui ne le traverse pas.
3. Les Solides Complexes
Les solides complexes sont des solides formés par la combinaison de plusieurs figures géométriques simples. Ils peuvent être composés de polyèdres, de corps ronds ou d’une combinaison des deux.
Propriétés des Figures Géométriques en 3D
Chaque figure géométrique en 3D possède un ensemble de propriétés spécifiques qui la définissent :
- Volume: Le volume d’un solide est la quantité d’espace qu’il occupe.
- Surface: La surface d’un solide est la somme des aires de toutes ses faces.
- Aires des Faces: Chaque face d’un polyèdre a une aire spécifique.
- Angles: Les angles entre les faces d’un polyèdre sont des angles solides.
- Symétrie: Certaines figures géométriques en 3D possèdent des axes de symétrie ou des plans de symétrie.
Création de Figures Géométriques en 3D
Il existe plusieurs méthodes pour créer des figures géométriques en 3D :
- Modélisation 3D: Des logiciels de modélisation 3D tels que Blender, Maya, ou 3ds Max permettent de créer des modèles numériques de figures géométriques en 3D.
- Impression 3D: L’impression 3D permet de créer des objets physiques à partir de modèles numériques 3D.
- Sculpture: La sculpture est une méthode traditionnelle de création de figures géométriques en 3D à partir de matériaux tels que la pierre, le bois ou l’argile.
Applications des Figures Géométriques en 3D
Les figures géométriques en 3D ont de nombreuses applications dans divers domaines :
- Architecture: Les architectes utilisent les figures géométriques en 3D pour concevoir des bâtiments, des ponts et d’autres structures.
- Ingénierie: Les ingénieurs utilisent les figures géométriques en 3D pour concevoir des machines, des véhicules et d’autres systèmes.
- Physique: Les physiciens utilisent les figures géométriques en 3D pour modéliser des phénomènes physiques tels que le mouvement des corps célestes.
- Art: Les artistes utilisent les figures géométriques en 3D pour créer des sculptures, des installations et des œuvres d’art numériques.
- Jeux vidéo: Les figures géométriques en 3D sont utilisées pour créer des environnements et des objets dans les jeux vidéo.
- Médecine: Les figures géométriques en 3D sont utilisées pour créer des modèles anatomiques et pour réaliser des interventions chirurgicales assistées par ordinateur.
Conclusion
Les figures géométriques en 3D sont des concepts fondamentaux qui jouent un rôle crucial dans de nombreux domaines. Comprendre leurs propriétés, leurs caractéristiques et leurs applications est essentiel pour progresser dans divers domaines scientifiques, techniques et artistiques.
Cet article n’a présenté qu’un aperçu de ce vaste sujet. Il existe de nombreux autres aspects des figures géométriques en 3D à explorer, tels que les propriétés topologiques, les théories de la géométrie non euclidienne, et les applications dans l’informatique et la robotique.
N’hésitez pas à poursuivre vos recherches et à découvrir les merveilles du monde tridimensionnel.

Figures Géométriques en 3D : Apprenez à Les Créer et Les Comprendre

Enregistrer un commentaire for "Figures Géométriques En 3D : Apprenez à Les Créer Et Les Comprendre"